Este teorema resulta de aplicar la regla de sustitución al problema de determinar la alteración que se produce en el régimen de intensidades de un circuito lineal cuando se da un incremento al parámetro que define uno de sus elementos pasivos. Se aplica extensamente para estudiar y comparar los errores posibles de los diferentes dispositivos de medida y para determinar las tolerancias de los parámetros constitutivos de un circuito en proyecto.
Sea el circuito activo de la Fig. 19a, por uno de cuyos elementos pasivos, de impedancia operacional Z(D), pasa una intensidad i1, y sea i2 la intensidad que pasa por otra rama cualquiera del circuito.
Representamos en la Fig. 19b el circuito resultante de cambiar Z(D) a Z(D)+ΔZ(D). Las intensidades i1 e i2 habrán experimentado, en consecuencia, unos incrementos que vamos a determinar.
Figura 19 (Click para ampliar)
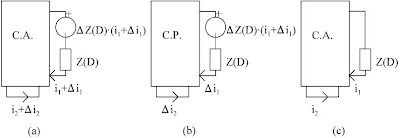
Aplicando la regla de sustitución al circuito de la Fig. 19b, podemos sustituir ΔZ(D) por una fuente de tensión:
e = ΔZ(D)A(i1 + Δi1)
tal como se representa en la Fig. 20a.
Figura 20 (Click para ampliar)
Por aplicación del teorema de superposición al circuito de la Fig 20a se tienen los circuitos de las Fig. 20b y 20c, de donde deducimos que Δi1 y Δi2 son las intensidades que resultan en las correspondientes ramas cuando sólo actúa esta fuente de tensión compensadora. Es decir, podemos calcular esos incrementos mediante el circuito de la Fig. 20b, en donde se han reducido a cero todas las fuentes ideales del circuito dado.
Para un estudio completo, que abarque incluso el periodo transitorio, se ha de tener en cuenta también en el circuito de la Fig. 20b la fuente de excitación equivalente a las condiciones iniciales en Z(D).
Podemos dar otra forma más útil de este teorema observando que la fuente definida por la ecuación e = ΔZ(D)A(i1 + )i1) es equivalente a otra fuente de tensión dada por ΔZ(D)·i1 en serie con una impedancia igual a )Z(D). Luego el circuito de la Fig. 21 nos sirve también para el cálculo de los incrementos en las intensidades debidas a la variación en la impedancia Z(D).
Este circuito tiene la ventaja sobre el de la Fig. 20b de que la fuente de tensión que utilizamos para el cálculo viene expresada en función de la intensidad primitiva,que es un dato, y no en función de la intensidad obtenida después de incrementarse Z(D), que es, precisamente, la incógnita.
Figura 21 (Click para ampliar)
Sea el circuito activo de la Fig. 19a, por uno de cuyos elementos pasivos, de impedancia operacional Z(D), pasa una intensidad i1, y sea i2 la intensidad que pasa por otra rama cualquiera del circuito.
Representamos en la Fig. 19b el circuito resultante de cambiar Z(D) a Z(D)+ΔZ(D). Las intensidades i1 e i2 habrán experimentado, en consecuencia, unos incrementos que vamos a determinar.
Figura 19 (Click para ampliar)Aplicando la regla de sustitución al circuito de la Fig. 19b, podemos sustituir ΔZ(D) por una fuente de tensión:
e = ΔZ(D)A(i1 + Δi1)
tal como se representa en la Fig. 20a.
Figura 20 (Click para ampliar)Por aplicación del teorema de superposición al circuito de la Fig 20a se tienen los circuitos de las Fig. 20b y 20c, de donde deducimos que Δi1 y Δi2 son las intensidades que resultan en las correspondientes ramas cuando sólo actúa esta fuente de tensión compensadora. Es decir, podemos calcular esos incrementos mediante el circuito de la Fig. 20b, en donde se han reducido a cero todas las fuentes ideales del circuito dado.
Para un estudio completo, que abarque incluso el periodo transitorio, se ha de tener en cuenta también en el circuito de la Fig. 20b la fuente de excitación equivalente a las condiciones iniciales en Z(D).
Podemos dar otra forma más útil de este teorema observando que la fuente definida por la ecuación e = ΔZ(D)A(i1 + )i1) es equivalente a otra fuente de tensión dada por ΔZ(D)·i1 en serie con una impedancia igual a )Z(D). Luego el circuito de la Fig. 21 nos sirve también para el cálculo de los incrementos en las intensidades debidas a la variación en la impedancia Z(D).
Este circuito tiene la ventaja sobre el de la Fig. 20b de que la fuente de tensión que utilizamos para el cálculo viene expresada en función de la intensidad primitiva,que es un dato, y no en función de la intensidad obtenida después de incrementarse Z(D), que es, precisamente, la incógnita.
Figura 21 (Click para ampliar)
0 comments:
Publicar un comentario