En esta seccion vamos a conocer algunos teoremas, reglas y principios de los más utilizados en Teoría de Circuitos. Algunos de ellos tienen demostración inmediata, pero otros exigen un proceso más detallado. En cualquier caso, solamente nos interesará conocerlos y comprobar su utilidad en ciertos casos concretos.
Principio de Superposición
Este principio, que se aplica a redes lineales, tiene por objeto calcular la respuesta en un elemento de un circuito, cuando existen varias fuentes, y dice lo siguiente:
La respuesta de un circuito lineal, a varias fuentes independientes de excitación actuando simultáneamente, es igual a la suma de las respuestas que se obtendrían cuando actuase cada una de ellas por separado.
La prueba de este Teorema puede establecerse directamente por un análisis de mallas, como vamos a ver analizando el circuito de la Fig. 1.
Figura 1 (Click para ampliar)
Ecuacion 1
de donde se deduce que, por ejemplo, la corriente i1 vale:
Ecuacion 2
donde Δ11 y Δ21 indican los menores adjuntos de la matriz de impedancias y Δz el determinante de la misma. Todas ellas son funciones de las impedancias de la red.
En general, para una red de n mallas, la corriente en una malla genérica j valdrá:
Ecuacion 3
en consecuencia, ij puede considerarse como la suma lineal de n componentes de corriente
Ecuacion 4
debidas a cada generador de malla vgk, actuando independientemente de las otras fuentes.
Debe hacerse notar que, para que deje de actuar un generador de tensión, debe anularse su tensión (vg = 0), es decir, se ha de cortocircuitar; mientras que para anular un generador de corriente (i = 0) se debe dejar abierto.
Debe tenerse en cuenta también que, al aplicar superposición, la potencia disipada en una resistencia no puede calcularse sumando las potencias debidas a las componentes individuales de corriente, sino que debe calcularse previamente la corriente total y, después, proceder al cálculo de potencia (P = I2·R).
Esto es así porque, como sabemos, la relación entre la potencia y la intensidad no es lineal sino cuadrática.
En general, la resolución de un circuito eléctrico por el principio de superposición es un procedimiento pesimista, ya que es bastante lento, comparado con el análisis de mallas o nudos. Sin embargo, cuando se tiene una red excitada con generadores de diferentes frecuencias, constituye el único procedimiento válido para determinar la respuesta del circuito.
Cuando se tienen fuentes dependientes en la red, éstas deben mantenerse intactas, debiendo figurar en cada uno de los circuitos en los que se desdobla la red. La razón de ello es que las fuentes dependientes, por su propia naturaleza, dependen de la tensión o corriente de alguna parte del circuito.
Veamos el ejemplo de la Fig. 2, donde nos piden obtener la potencia disipada por la resistencia de 3Ω.
Figura 2 (Click para ampliar)
Analizaremos los dos circuitos de la Fig. 3, en los cuales siempre se considera la fuente dependiente y, únicamente, un generador independiente.
Figura 3 (Click para ampliar)
Para la Fig. 3a se tiene: 12 - 2i1 = (3+1)i1 → i1 = 2A
Para la Fig. 2b se tiene: -2i2 = 1·i2 + 3(i2 + 6) → i2 = -3A
La corriente que circula por la resistencia de 3Ω será:
i(3Ω) = i1 + (i2 + 6) = 2 + (-3 + 6) = 5A → P = 3·i2 = 75 w
La respuesta de un circuito lineal, a varias fuentes independientes de excitación actuando simultáneamente, es igual a la suma de las respuestas que se obtendrían cuando actuase cada una de ellas por separado.
La prueba de este Teorema puede establecerse directamente por un análisis de mallas, como vamos a ver analizando el circuito de la Fig. 1.
Figura 1 (Click para ampliar)
Ecuacion 1de donde se deduce que, por ejemplo, la corriente i1 vale:
Ecuacion 2donde Δ11 y Δ21 indican los menores adjuntos de la matriz de impedancias y Δz el determinante de la misma. Todas ellas son funciones de las impedancias de la red.
En general, para una red de n mallas, la corriente en una malla genérica j valdrá:
Ecuacion 3en consecuencia, ij puede considerarse como la suma lineal de n componentes de corriente
Ecuacion 4debidas a cada generador de malla vgk, actuando independientemente de las otras fuentes.
Debe hacerse notar que, para que deje de actuar un generador de tensión, debe anularse su tensión (vg = 0), es decir, se ha de cortocircuitar; mientras que para anular un generador de corriente (i = 0) se debe dejar abierto.
Debe tenerse en cuenta también que, al aplicar superposición, la potencia disipada en una resistencia no puede calcularse sumando las potencias debidas a las componentes individuales de corriente, sino que debe calcularse previamente la corriente total y, después, proceder al cálculo de potencia (P = I2·R).
Esto es así porque, como sabemos, la relación entre la potencia y la intensidad no es lineal sino cuadrática.
En general, la resolución de un circuito eléctrico por el principio de superposición es un procedimiento pesimista, ya que es bastante lento, comparado con el análisis de mallas o nudos. Sin embargo, cuando se tiene una red excitada con generadores de diferentes frecuencias, constituye el único procedimiento válido para determinar la respuesta del circuito.
Cuando se tienen fuentes dependientes en la red, éstas deben mantenerse intactas, debiendo figurar en cada uno de los circuitos en los que se desdobla la red. La razón de ello es que las fuentes dependientes, por su propia naturaleza, dependen de la tensión o corriente de alguna parte del circuito.
Veamos el ejemplo de la Fig. 2, donde nos piden obtener la potencia disipada por la resistencia de 3Ω.
Figura 2 (Click para ampliar)Analizaremos los dos circuitos de la Fig. 3, en los cuales siempre se considera la fuente dependiente y, únicamente, un generador independiente.
Figura 3 (Click para ampliar)Para la Fig. 3a se tiene: 12 - 2i1 = (3+1)i1 → i1 = 2A
Para la Fig. 2b se tiene: -2i2 = 1·i2 + 3(i2 + 6) → i2 = -3A
La corriente que circula por la resistencia de 3Ω será:
i(3Ω) = i1 + (i2 + 6) = 2 + (-3 + 6) = 5A → P = 3·i2 = 75 w
Teorema de Helmholtz-Thevenin
El conocido teorema de Thévenin fue estudiado a mediados del siglo pasado por Helmholtz (en 1.853 y, por cierto, en forma más general: para una red activa con N bornes externos). Olvidado, se ha visto revalorizado en el presente siglo. Redescubierto en 1.883 por Thévenin, es conocido más comúnmente bajo este nombre.
Cuando el interés en el estudio de una red se fija en una parte de la misma, por ejemplo en una rama, es interesante poder separar esta rama del resto de la red para no tener que resolver el circuito completo cada vez que se modifiquen los parámetros de esa rama.
Su enunciado podría ser:
Cualquier red lineal, compuesta por elementos pasivos y activos (dependientes o independientes) se puede sustituir (desde el punto de vista de sus terminales externos AB) por un generador de tensión Vth denominado generador de Thévenin, más una impedancia en serie Zth
(véase Fig. 4).
Figura 4 (Click para ampliar)
En la Fig. 4b se muestra el circuito equivalente de Thévenin de la red dipolo de la Fig. 4a.
Si ambas redes han de ser equivalentes deberán tener los mismos valores de tensión y corriente, a una impedancia de carga ZL. Está claro que para calcular los valores de Vth y Zth se necesitarán fijar dos condiciones específicas en el valor de ZL; y las más simples serán ZL = ∞ y ZL = 0.
El hacer ZL = ∞ significa físicamente desconectar la impedancia de carga del circuito. En esta situación, el circuito de la Fig. 4a dará una tensión en vacío o circuito abierto V0, con i = 0, que deberá ser idéntica a la que debe dar el circuito de la Fig. 4b; en este circuito, si i = 0, se obtiene una tensión entre los terminales AB igual a Vth, ya que la caída de tensión en la Zth será nula.
Por consiguiente:
El valor de Vth de la red equivalente es igual a la magnitud V0 de la red lineal que se obtiene entre los terminales de salida AB al desconectar la carga y dejar el circuito abierto.
Si ahora se elige ZL = 0, que representa un cortocircuito entre los terminales externos y denominamos icorto a la corriente que circula por este cortocircuito realizado entre los terminales AB del circuito de la Fig. 4a, se deberá obtener la misma corriente icorto para el circuito de la Fig. 4b. En esta figura ZL = 0, con lo que:
Ecuacion 5
de donde se obtiene el valor de Zth:
Ecuacion 6
El valor de Zth se obtiene como cociente entre la tensión que da la red en vacío V0 = Vth y la corriente de cortocircuito icorto.
Si los generadores de la red lineal (Fig. 4a) son todos independientes, el cálculo de Zth es más simple que el expresado en la última ecuación, y representa el valor de la impedancia que se observa entre los terminales A y B de salida cuando se anulan los generadores internos (es decir, se cortocircuitan los generadores de tensión y se abren los de corriente). Téngase en cuenta que si se anulan los generadores de la red, al no existir fuentes de excitación, darán lugar a una tensión equivalente de Thévenin igual a cero, y según el circuito de la Fig. 4b, al anular Vth, la impedancia que se observa entre los terminales A y B (quitando, por supuesto, la carga) coincide con Zth.
Cuando la red lineal contiene generadores dependientes, éstos no se pueden anular, ya que sus amplitudes dependen de alguna variable de tensión o corriente de la red y, por ello, la determinación de Zth debe realizarse de acuerdo con la definición general (Vth/icorto). En este caso, es frecuente encontrar valores negativos para la impedancia de Thévenin, que no tiene sentido físico, pero sí matemático.
Cuando el interés en el estudio de una red se fija en una parte de la misma, por ejemplo en una rama, es interesante poder separar esta rama del resto de la red para no tener que resolver el circuito completo cada vez que se modifiquen los parámetros de esa rama.
Su enunciado podría ser:
Cualquier red lineal, compuesta por elementos pasivos y activos (dependientes o independientes) se puede sustituir (desde el punto de vista de sus terminales externos AB) por un generador de tensión Vth denominado generador de Thévenin, más una impedancia en serie Zth
(véase Fig. 4).
Figura 4 (Click para ampliar)En la Fig. 4b se muestra el circuito equivalente de Thévenin de la red dipolo de la Fig. 4a.
Si ambas redes han de ser equivalentes deberán tener los mismos valores de tensión y corriente, a una impedancia de carga ZL. Está claro que para calcular los valores de Vth y Zth se necesitarán fijar dos condiciones específicas en el valor de ZL; y las más simples serán ZL = ∞ y ZL = 0.
El hacer ZL = ∞ significa físicamente desconectar la impedancia de carga del circuito. En esta situación, el circuito de la Fig. 4a dará una tensión en vacío o circuito abierto V0, con i = 0, que deberá ser idéntica a la que debe dar el circuito de la Fig. 4b; en este circuito, si i = 0, se obtiene una tensión entre los terminales AB igual a Vth, ya que la caída de tensión en la Zth será nula.
Por consiguiente:
El valor de Vth de la red equivalente es igual a la magnitud V0 de la red lineal que se obtiene entre los terminales de salida AB al desconectar la carga y dejar el circuito abierto.
Si ahora se elige ZL = 0, que representa un cortocircuito entre los terminales externos y denominamos icorto a la corriente que circula por este cortocircuito realizado entre los terminales AB del circuito de la Fig. 4a, se deberá obtener la misma corriente icorto para el circuito de la Fig. 4b. En esta figura ZL = 0, con lo que:
Ecuacion 5de donde se obtiene el valor de Zth:
Ecuacion 6El valor de Zth se obtiene como cociente entre la tensión que da la red en vacío V0 = Vth y la corriente de cortocircuito icorto.
Si los generadores de la red lineal (Fig. 4a) son todos independientes, el cálculo de Zth es más simple que el expresado en la última ecuación, y representa el valor de la impedancia que se observa entre los terminales A y B de salida cuando se anulan los generadores internos (es decir, se cortocircuitan los generadores de tensión y se abren los de corriente). Téngase en cuenta que si se anulan los generadores de la red, al no existir fuentes de excitación, darán lugar a una tensión equivalente de Thévenin igual a cero, y según el circuito de la Fig. 4b, al anular Vth, la impedancia que se observa entre los terminales A y B (quitando, por supuesto, la carga) coincide con Zth.
Cuando la red lineal contiene generadores dependientes, éstos no se pueden anular, ya que sus amplitudes dependen de alguna variable de tensión o corriente de la red y, por ello, la determinación de Zth debe realizarse de acuerdo con la definición general (Vth/icorto). En este caso, es frecuente encontrar valores negativos para la impedancia de Thévenin, que no tiene sentido físico, pero sí matemático.
Teorema de Helmholtz-Norton
El teorema de Thévenin tiene una versión dual que es el teorema de Norton. En este caso la red lineal de la Fig. 5a se puede sustituir por un generador de corriente iN en paralelo con una impedancia ZN (Fig. 5b).
Figura 5 (Click para ampliar)
En definitiva, esta equivalencia representa, al comparar las Fig. 4b y Fig. 5b, la sustitución de un generador de tensión por otro de corriente. Así observamos que se debe cumplir:
Ecuacion 7
que nos indica que el generador de corriente de Norton es igual a la corriente de cortocircuito que se obtiene en la red al juntar sus terminales (ZL = 0) y que la impedancia de Norton es el cociente entre la tensión en vacío y la corriente de cortocircuito de la red (al igual que la impedancia de Thévenin).
El trabajo de Norton fue publicado 50 años después que el de Thévenin.
Figura 5 (Click para ampliar)En definitiva, esta equivalencia representa, al comparar las Fig. 4b y Fig. 5b, la sustitución de un generador de tensión por otro de corriente. Así observamos que se debe cumplir:
Ecuacion 7que nos indica que el generador de corriente de Norton es igual a la corriente de cortocircuito que se obtiene en la red al juntar sus terminales (ZL = 0) y que la impedancia de Norton es el cociente entre la tensión en vacío y la corriente de cortocircuito de la red (al igual que la impedancia de Thévenin).
El trabajo de Norton fue publicado 50 años después que el de Thévenin.
Teorema de Millman
Este teorema permite calcular la tensión UAB que existe entre dos nudos A y B, conociendo las impedancias que concurren en B y las tensiones entre el nudo A y los otros extremos de las citadas impedancias (véase Fig. 6). Esto es, suponemos conocidas UA1, UA2, ..., UAn aunque pueda ignorarse la configuración de la red entre A y los otros nudos.
Apliquemos la regla obtenida en el método de análisis por nudos y escribamos la ecuación nodal del nudo B, tomando A como nudo de referencia. Se obtiene así:
Figura 6 (Click para ampliar)
(Y1 + Y2 + ...+ Yn)·UBA - Y1U1A - Y2U2A - ...-YnUnA = 0
es decir:
Ecuacion 8
ya que no existe intensidad de alimentación de nudo.
Teniendo en cuenta que UBA = -UAB y UKA = -UAK se deduce que:
Ecuacion 9
fórmula que constituye la expresión del teorema de Millman. El nudo A puede ser una cualquiera del circuito y, por tanto, puede ser alguno de los nudos 1, 2, ..., n. En este caso particular, será nulo el término correspondiente de:
El caso de n fuentes de tensión reales en paralelo (Fig. 7) es un caso particular en que podemos usar este teorema.
Figura 7 (Click para ampliar)
Aplicando el teorema de Millman:
Ecuacion 10
Apliquemos la regla obtenida en el método de análisis por nudos y escribamos la ecuación nodal del nudo B, tomando A como nudo de referencia. Se obtiene así:
Figura 6 (Click para ampliar)(Y1 + Y2 + ...+ Yn)·UBA - Y1U1A - Y2U2A - ...-YnUnA = 0
es decir:
Ecuacion 8ya que no existe intensidad de alimentación de nudo.
Teniendo en cuenta que UBA = -UAB y UKA = -UAK se deduce que:
Ecuacion 9fórmula que constituye la expresión del teorema de Millman. El nudo A puede ser una cualquiera del circuito y, por tanto, puede ser alguno de los nudos 1, 2, ..., n. En este caso particular, será nulo el término correspondiente de:
El caso de n fuentes de tensión reales en paralelo (Fig. 7) es un caso particular en que podemos usar este teorema.
Figura 7 (Click para ampliar)Aplicando el teorema de Millman:
Ecuacion 10Teorema de Rosen
Un circuito pasivo constituido por n impedancias Z1, Z2, ..., Zn conectadas en estrella (Fig. 8), puede ser sustituido por otro circuito equivalente formado por n(n-1)/2 impedancias Z12, Z13, ..., Z1n, Z23, ..., Z2n, ..., Zmn conectadas en polígono (Fig. 9).
Figura 8 (Click para ampliar)
La equivalencia se refiere a la posible conexión a otro circuito externo, de la totalidad o parte de los n terminales 1, 2, ...n.
Exceptuaremos el centro N de la estrella, que no existe en la configuración polígono.
Dicha equivalencia quedará probada si las intensidades i1, i2, ..., in salientes de los nudos son iguales en las dos configuraciones para todo conjunto de tensiones u1, u2, ..., un de dichos terminales, que actúe sobre ambas. Estas tensiones de los terminales son respecto de un punto cualquiera de referencia (representamos la conexión externa por un circuito activo C.A.).
Figura 9 (Click para ampliar)
Puede verse que esas intensidades son iguales si:
Ecuacion 11
Veamos algunos casos particulares como aplicación.
a) n=2 : Resistencias en serie.
En este caso el polígono estará formado por 2·(2-1)/2 = 1 resistencia.
Figura 10
b) n = 3 (Estrella-Triángulo).
Figura 11
En este caso tendremos 3(3-1)/2 = 3 resistencias en triángulo.
Ecuacion 12
c)n = 4 :
Ahora tendremos 4(4-1)/2 = 6 resistencias en polígono.
Figura 12
Las admitancias del polígono serán:
Ecuacion 13
Dado un polígono de impedancias, no siempre es posible el cálculo de una estrella equivalente.
Para n = 2, resulta evidente que dada Z12 en la ecuación, existen infinitos valores de las incógnitas Z1 y Z2 que cumplen que Z1 + Z2 = Z12.
Para n = 3 tenemos tres ecuaciones con tres incógnitas, siendo la solución única (ya vimos que dado el triángulo, la estrella equivalente está determinada).
Para n = 4 disponemos de seis ecuaciones con cuatro incógnitas, por lo que el sistema puede ser incompatible (si el polígono proviene de una estrella se tendrán otras dos relaciones:
Y12Y34 = Y13Y24 = Y14Y23) que nos permitirán calcular los elementos de la estrella equivalente.
Figura 8 (Click para ampliar)La equivalencia se refiere a la posible conexión a otro circuito externo, de la totalidad o parte de los n terminales 1, 2, ...n.
Exceptuaremos el centro N de la estrella, que no existe en la configuración polígono.
Dicha equivalencia quedará probada si las intensidades i1, i2, ..., in salientes de los nudos son iguales en las dos configuraciones para todo conjunto de tensiones u1, u2, ..., un de dichos terminales, que actúe sobre ambas. Estas tensiones de los terminales son respecto de un punto cualquiera de referencia (representamos la conexión externa por un circuito activo C.A.).
Figura 9 (Click para ampliar)Puede verse que esas intensidades son iguales si:
Ecuacion 11Veamos algunos casos particulares como aplicación.
a) n=2 : Resistencias en serie.
En este caso el polígono estará formado por 2·(2-1)/2 = 1 resistencia.
Figura 10b) n = 3 (Estrella-Triángulo).
Figura 11En este caso tendremos 3(3-1)/2 = 3 resistencias en triángulo.
Ecuacion 12c)n = 4 :
Ahora tendremos 4(4-1)/2 = 6 resistencias en polígono.
Figura 12Las admitancias del polígono serán:
Ecuacion 13Dado un polígono de impedancias, no siempre es posible el cálculo de una estrella equivalente.
Para n = 2, resulta evidente que dada Z12 en la ecuación, existen infinitos valores de las incógnitas Z1 y Z2 que cumplen que Z1 + Z2 = Z12.
Para n = 3 tenemos tres ecuaciones con tres incógnitas, siendo la solución única (ya vimos que dado el triángulo, la estrella equivalente está determinada).
Para n = 4 disponemos de seis ecuaciones con cuatro incógnitas, por lo que el sistema puede ser incompatible (si el polígono proviene de una estrella se tendrán otras dos relaciones:
Y12Y34 = Y13Y24 = Y14Y23) que nos permitirán calcular los elementos de la estrella equivalente.
Teorema de Reciprocidad
a)Primer enunciado:
La tensión Upq (Fig. 13a) que aparece entre dos nudos (p, q) de un circuito lineal y pasivo cuando se aplica una fuente de intensidad i entre otro par de nudos (m, n) es igual a la tensión Umn (Fig. 13b) que origina la misma fuente trasladada al par de nudos (p, q).
Figura 13 (Click para ampliar)
b)Segundo enunciado:
La intensidad i (Fig. 14a) que circula por una rama de un circuito lineal y pasivo, cuando se intercala una fuente de tensión en otra rama, es la misma que circularía (Fig. 14b) por esta última si la fuente de tensión se intercalase en la primera.
Figura 14 (Click para ampliar)
La tensión Upq (Fig. 13a) que aparece entre dos nudos (p, q) de un circuito lineal y pasivo cuando se aplica una fuente de intensidad i entre otro par de nudos (m, n) es igual a la tensión Umn (Fig. 13b) que origina la misma fuente trasladada al par de nudos (p, q).
Figura 13 (Click para ampliar)b)Segundo enunciado:
La intensidad i (Fig. 14a) que circula por una rama de un circuito lineal y pasivo, cuando se intercala una fuente de tensión en otra rama, es la misma que circularía (Fig. 14b) por esta última si la fuente de tensión se intercalase en la primera.
Figura 14 (Click para ampliar)Regla de Sustitución. Teorema de Miller
Si se conoce la relación u = Z(D)·i ó i = Y(D)·u entre los terminales de un elemento pasivo o de una rama de un circuito, estos elementos pueden sustituirse por una fuente de tensión, cuya forma de onda sea Z(D)·i, o por una fuente de intensidad dada por Y(D)·u.
Figura 15 (Click para ampliar)
Esta regla está fundada en que la sustitución indicada no altera las ecuaciones que se deducen a partir de las Leyes de Kirchhoff.
Estas fuentes de sustitución son dependientes y ha de tenerse en cuenta que se comportan de forma distinta que las fuentes ideales. En particular se puede explicar esta regla a un circuito abierto y a un circuito en corto.
Si la tensión entre dos terminales A y B de un circuito activo es Uo, no se altera en nada el estado del circuito al conectar esos terminales mediante una fuente de tensión e0 = Uo de la misma polaridad que la existente entre A y B (Fig. 16).
Figura 16 (Click para ampliar)
Su configuración cambia aparentemente, pues aumenta en una unidad el número de mallas, pero ha de tenerse en cuenta que en esa malla no circula intensidad alguna, luego no aumenta el número de incógnitas.
Análogamente, en un conductor de resistencia nula, por el que circula una intensidad i0, puede intercalarse una fuente ideal de intensidad igual a i0 sin que se altere el estado del circuito.
Un condensador con carga eléctrica inicial o una bobina con flujo inicial admiten una representación sencilla haciendo uso de la regla de sustitución. En el caso de un condensador cargado inicialmente a una tensión Uo, la ecuación de definición es:
Ecuacion 14
que corresponde al circuito de la Fig. 17a.
Figura 17 (Click para ampliar)
Es decir, se sustituye por una fuente de tensión en serie con un condensador inicialmente descargado.
Para una bobina por la que circula inicialmente una intensidad I0, la ecuación de definición es:
Ecuacion 15
que corresponde al circuito de la Fig. 17b.
La regla de sustitución es una herramienta muy útil en la demostración de teoremas. Por ejemplo el Teorema de Miller (en Electrónica):
Si en un circuito como el de la Fig.18a se sustituye la impedancia Z por un circuito abierto y se une el nudo 1 a otro 0, este último tomado como referencia, mediante una impedancia Z/(1-k) y el 2 se une también al mismo nudo O por medio de otra impedancia de valor ZK/(k-1), en donde k es la relación U2/U1 entre las tensiones de los nudos 2 y 1 respecto a 0, no se altera la intensidad que circula entre los nudos 1 y 2. (Fig. 18b).
Figura 18 (Click para ampliar)
Figura 15 (Click para ampliar)Esta regla está fundada en que la sustitución indicada no altera las ecuaciones que se deducen a partir de las Leyes de Kirchhoff.
Estas fuentes de sustitución son dependientes y ha de tenerse en cuenta que se comportan de forma distinta que las fuentes ideales. En particular se puede explicar esta regla a un circuito abierto y a un circuito en corto.
Si la tensión entre dos terminales A y B de un circuito activo es Uo, no se altera en nada el estado del circuito al conectar esos terminales mediante una fuente de tensión e0 = Uo de la misma polaridad que la existente entre A y B (Fig. 16).
Figura 16 (Click para ampliar)Su configuración cambia aparentemente, pues aumenta en una unidad el número de mallas, pero ha de tenerse en cuenta que en esa malla no circula intensidad alguna, luego no aumenta el número de incógnitas.
Análogamente, en un conductor de resistencia nula, por el que circula una intensidad i0, puede intercalarse una fuente ideal de intensidad igual a i0 sin que se altere el estado del circuito.
Un condensador con carga eléctrica inicial o una bobina con flujo inicial admiten una representación sencilla haciendo uso de la regla de sustitución. En el caso de un condensador cargado inicialmente a una tensión Uo, la ecuación de definición es:
Ecuacion 14que corresponde al circuito de la Fig. 17a.
Figura 17 (Click para ampliar)Es decir, se sustituye por una fuente de tensión en serie con un condensador inicialmente descargado.
Para una bobina por la que circula inicialmente una intensidad I0, la ecuación de definición es:
Ecuacion 15que corresponde al circuito de la Fig. 17b.
La regla de sustitución es una herramienta muy útil en la demostración de teoremas. Por ejemplo el Teorema de Miller (en Electrónica):
Si en un circuito como el de la Fig.18a se sustituye la impedancia Z por un circuito abierto y se une el nudo 1 a otro 0, este último tomado como referencia, mediante una impedancia Z/(1-k) y el 2 se une también al mismo nudo O por medio de otra impedancia de valor ZK/(k-1), en donde k es la relación U2/U1 entre las tensiones de los nudos 2 y 1 respecto a 0, no se altera la intensidad que circula entre los nudos 1 y 2. (Fig. 18b).
Figura 18 (Click para ampliar)Teorema de Compensación
Este teorema resulta de aplicar la regla de sustitución al problema de determinar la alteración que se produce en el régimen de intensidades de un circuito lineal cuando se da un incremento al parámetro que define uno de sus elementos pasivos. Se aplica extensamente para estudiar y comparar los errores posibles de los diferentes dispositivos de medida y para determinar las tolerancias de los parámetros constitutivos de un circuito en proyecto.
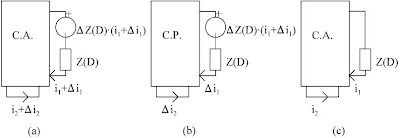
Sea el circuito activo de la Fig. 19a, por uno de cuyos elementos pasivos, de impedancia operacional Z(D), pasa una intensidad i1, y sea i2 la intensidad que pasa por otra rama cualquiera del circuito.
Representamos en la Fig. 19b el circuito resultante de cambiar Z(D) a Z(D)+ΔZ(D). Las intensidades i1 e i2 habrán experimentado, en consecuencia, unos incrementos que vamos a determinar.
Figura 19 (Click para ampliar)
Aplicando la regla de sustitución al circuito de la Fig. 19b, podemos sustituir ΔZ(D) por una fuente de tensión:
e = ΔZ(D)A(i1 + Δi1)
tal como se representa en la Fig. 20a.
Figura 20 (Click para ampliar)
Por aplicación del teorema de superposición al circuito de la Fig 20a se tienen los circuitos de las Fig. 20b y 20c, de donde deducimos que Δi1 y Δi2 son las intensidades que resultan en las correspondientes ramas cuando sólo actúa esta fuente de tensión compensadora. Es decir, podemos calcular esos incrementos mediante el circuito de la Fig. 20b, en donde se han reducido a cero todas las fuentes ideales del circuito dado.
Para un estudio completo, que abarque incluso el periodo transitorio, se ha de tener en cuenta también en el circuito de la Fig. 20b la fuente de excitación equivalente a las condiciones iniciales en Z(D).
Podemos dar otra forma más útil de este teorema observando que la fuente definida por la ecuación e = ΔZ(D)A(i1 + )i1) es equivalente a otra fuente de tensión dada por ΔZ(D)·i1 en serie con una impedancia igual a )Z(D). Luego el circuito de la Fig. 21 nos sirve también para el cálculo de los incrementos en las intensidades debidas a la variación en la impedancia Z(D).
Este circuito tiene la ventaja sobre el de la Fig. 20b de que la fuente de tensión que utilizamos para el cálculo viene expresada en función de la intensidad primitiva,que es un dato, y no en función de la intensidad obtenida después de incrementarse Z(D), que es, precisamente, la incógnita.
Figura 21 (Click para ampliar)
Sea el circuito activo de la Fig. 19a, por uno de cuyos elementos pasivos, de impedancia operacional Z(D), pasa una intensidad i1, y sea i2 la intensidad que pasa por otra rama cualquiera del circuito.
Representamos en la Fig. 19b el circuito resultante de cambiar Z(D) a Z(D)+ΔZ(D). Las intensidades i1 e i2 habrán experimentado, en consecuencia, unos incrementos que vamos a determinar.
Figura 19 (Click para ampliar)Aplicando la regla de sustitución al circuito de la Fig. 19b, podemos sustituir ΔZ(D) por una fuente de tensión:
e = ΔZ(D)A(i1 + Δi1)
tal como se representa en la Fig. 20a.
Figura 20 (Click para ampliar)Por aplicación del teorema de superposición al circuito de la Fig 20a se tienen los circuitos de las Fig. 20b y 20c, de donde deducimos que Δi1 y Δi2 son las intensidades que resultan en las correspondientes ramas cuando sólo actúa esta fuente de tensión compensadora. Es decir, podemos calcular esos incrementos mediante el circuito de la Fig. 20b, en donde se han reducido a cero todas las fuentes ideales del circuito dado.
Para un estudio completo, que abarque incluso el periodo transitorio, se ha de tener en cuenta también en el circuito de la Fig. 20b la fuente de excitación equivalente a las condiciones iniciales en Z(D).
Podemos dar otra forma más útil de este teorema observando que la fuente definida por la ecuación e = ΔZ(D)A(i1 + )i1) es equivalente a otra fuente de tensión dada por ΔZ(D)·i1 en serie con una impedancia igual a )Z(D). Luego el circuito de la Fig. 21 nos sirve también para el cálculo de los incrementos en las intensidades debidas a la variación en la impedancia Z(D).
Este circuito tiene la ventaja sobre el de la Fig. 20b de que la fuente de tensión que utilizamos para el cálculo viene expresada en función de la intensidad primitiva,que es un dato, y no en función de la intensidad obtenida después de incrementarse Z(D), que es, precisamente, la incógnita.
Figura 21 (Click para ampliar)
