En ocasiones, debido en general a hipótesis simplificadoras, podrán aparecer en un circuito ramas activas en que se tiene un elemento en serie con un generador de intensidad ideal, o bien un generador de tensión ideal en paralelo con otro elemento. En ambos casos, ya vimos que, a efectos del resto de circuito, esos elementos pueden quitarse en el análisis, por lo que volveríamos a tener la Fig. 6. (Esto es válido siempre que el elemento no presente acoplamiento magnético con el resto del circuito).
En cuanto a asociaciones de generadores de tensión entre sí o de intensidad, ya vimos las situaciones posibles y las que no lo son. Para poder efectuar la transformación de fuentes es necesario la existencia de un elemento pasivo en serie con la fuente de tensión o en paralelo con la de intensidad.
En el caso de que una rama de un circuito esté formada por una fuente ideal de tensión, dependiente o independiente, sin ningún elemento en serie, estudiaremos la forma de eliminar dicha rama sin que varíe la tensión e intensidad en el resto de los elementos del circuito. Igualmente, caso de que una rama de un circuito esté formada por una fuente ideal de intensidad, dependiente o independiente, sin ningún elemento en paralelo, estudiaremos la forma de eliminar dicha rama sin que varíe la tensión e intensidad en el resto de los elementos del circuito.
Figura 7 (Click para ampliar)
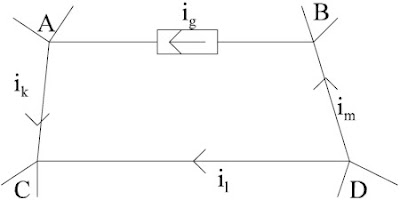
Consideremos primero este segundo caso, representado en la Fig. 7,donde la rama A-B está formada por una fuente de intensidad, ig. Las ramas k, l y m de la citada figura son un conjunto de ramas que forman un lazo con dicha rama A-B. La fuente de intensidad excita el resto del circuito introduciendo por A una intensidad ig que extrae de B.
Figura 8 (Click para ampliar)
Esto mismo se consigue en el circuito transformado de la Fig. 8, ya que ig entra y sale de C y D y las fuentes no aportan nada a estos nudos. En consecuencia, a excepción de la fuente de intensidad, todos los restantes elementos del circuito se comportarán igualmente y, por tanto, la tensión uAB será la misma en ambos. Una vez resuelto el circuito de la Fig. 8, la tensión de la fuente del circuito original (Fig. 7) se puede obtener teniendo en cuenta que
que multiplicando ambos miembros por ig nos indica que la potencia suministrada coincide con la suma de las potencias entregadas a cada rama.
El lazo elegido en la Fig. 8 para transportar la intensidad ig desde el nudo B al A, mediante fuentes de intensidad en paralelo con ramas del mismo, puede ser cualquiera que se cierre sobre la rama A-B.
Figura 9 (Click para ampliar)
Consideremos ahora el caso representado en la Fig. 9, donde la rama A-B está formada por una fuente ideal de tensión eg. Las ramas k, l y m de la citada figura son el conjunto de todas las ramas que, junto con la A-B, concurren en uno de los extremos de ésta. La fuente de tensión excita el resto del circuito haciendo que el potencial de B exceda al de A en uBA = eg.
Figura 10 (Click para ampliar)
En el circuito transformado de la Fig. 10, los nudos Bk, Bl y Bm están todos al mismo potencial uBA = eg respecto de A, por lo que da igual considerarlos unidos o separados. Esto es, el sistema de tres fuentes iguales de la Fig. 10 excita al resto del circuito de igual forma que una sola fuente de la Fig. 9. En consecuencia, los elementos externos a la fuente se comportan igualmente en una y otra configuración. Se observa que iAB = ik -il + im con lo que, multiplicando ambos miembros por eg, llegamos a que la potencia suministrada por la fuente del circuito de la Fig. 9 es igual a la suministrada por las fuentes del circuito de la Fig. 10, con lo que se comprueba que el circuito conectado a las fuentes recibe la misma aportación energética en uno y otro caso.
En cuanto a asociaciones de generadores de tensión entre sí o de intensidad, ya vimos las situaciones posibles y las que no lo son. Para poder efectuar la transformación de fuentes es necesario la existencia de un elemento pasivo en serie con la fuente de tensión o en paralelo con la de intensidad.
En el caso de que una rama de un circuito esté formada por una fuente ideal de tensión, dependiente o independiente, sin ningún elemento en serie, estudiaremos la forma de eliminar dicha rama sin que varíe la tensión e intensidad en el resto de los elementos del circuito. Igualmente, caso de que una rama de un circuito esté formada por una fuente ideal de intensidad, dependiente o independiente, sin ningún elemento en paralelo, estudiaremos la forma de eliminar dicha rama sin que varíe la tensión e intensidad en el resto de los elementos del circuito.
Figura 7 (Click para ampliar)Consideremos primero este segundo caso, representado en la Fig. 7,donde la rama A-B está formada por una fuente de intensidad, ig. Las ramas k, l y m de la citada figura son un conjunto de ramas que forman un lazo con dicha rama A-B. La fuente de intensidad excita el resto del circuito introduciendo por A una intensidad ig que extrae de B.
Figura 8 (Click para ampliar)Esto mismo se consigue en el circuito transformado de la Fig. 8, ya que ig entra y sale de C y D y las fuentes no aportan nada a estos nudos. En consecuencia, a excepción de la fuente de intensidad, todos los restantes elementos del circuito se comportarán igualmente y, por tanto, la tensión uAB será la misma en ambos. Una vez resuelto el circuito de la Fig. 8, la tensión de la fuente del circuito original (Fig. 7) se puede obtener teniendo en cuenta que
que multiplicando ambos miembros por ig nos indica que la potencia suministrada coincide con la suma de las potencias entregadas a cada rama.
El lazo elegido en la Fig. 8 para transportar la intensidad ig desde el nudo B al A, mediante fuentes de intensidad en paralelo con ramas del mismo, puede ser cualquiera que se cierre sobre la rama A-B.
Figura 9 (Click para ampliar)Consideremos ahora el caso representado en la Fig. 9, donde la rama A-B está formada por una fuente ideal de tensión eg. Las ramas k, l y m de la citada figura son el conjunto de todas las ramas que, junto con la A-B, concurren en uno de los extremos de ésta. La fuente de tensión excita el resto del circuito haciendo que el potencial de B exceda al de A en uBA = eg.
Figura 10 (Click para ampliar)En el circuito transformado de la Fig. 10, los nudos Bk, Bl y Bm están todos al mismo potencial uBA = eg respecto de A, por lo que da igual considerarlos unidos o separados. Esto es, el sistema de tres fuentes iguales de la Fig. 10 excita al resto del circuito de igual forma que una sola fuente de la Fig. 9. En consecuencia, los elementos externos a la fuente se comportan igualmente en una y otra configuración. Se observa que iAB = ik -il + im con lo que, multiplicando ambos miembros por eg, llegamos a que la potencia suministrada por la fuente del circuito de la Fig. 9 es igual a la suministrada por las fuentes del circuito de la Fig. 10, con lo que se comprueba que el circuito conectado a las fuentes recibe la misma aportación energética en uno y otro caso.
0 comments:
Publicar un comentario