Consideraremos ahora las expresiones de la potencia y de la energía en los diferentes elementos de los circuitos.
Resistencia
Para las referencias tomadas en la Fig. 3 tenemos:
Ecuación de definición:
Potencia entrante:
Sustituyendo (6) en (7) se llega a:
y, por tanto:
La energía absorbida por una resistencia es siempre positiva y es disipada en forma de calor (Ley de Joule).
Condensador
A partir de su ecuación de definición:
para las referencias de la Fig. 4 y de la expresión de potencia entrante, obtenemos:
luego:
En todo condensador físico u(-∞) = 0, luego:
Como se observa, el valor de la energía del condensador en uun instante determinado solo depende del valor de la tensión en dicho instante, pero no de la forma como varía ésta. Igualmente, podemos comprobar que la tensión del condensador no puede variar bruscamente, ya que, si así fuera, también lo haría la energía, lo cual implicaría una potencia infinita en el punto de discontinuidad, cosa físicamente imposible.
Toda energía absorbida por el condensador es almacenada en el campo eléctrico existente entre sus armaduras. Siendo q = C·u, podemos obtener otras expresiones:
Por otro lado, todo condensador es capaz de ceder energía a costa de la que ya había absorbido previamente. Ello ocurre, por ejemplo, en la descarga de un condensador a través de una resistencia.
Bobina Ideal
Para las referencias de la Fig. 5 tenemos:
Ecuación de definición:
Potencia entrante:
por tanto:
En toda bobina física i(-∞) = 0, luego:
La ecuacion 18 nos muestra que el valor de la energía absorbida por la bobina en un instante dado sólo depende del valor de la intensidad en dicho instante y no de la forma como varía ésta. Por otro lado, comprobamos que la intensidad de la bobina no puede presentar discontinuidades, ya que si fuera así, también las presentaría la energía, con el consiguiente valor infinito de la potencia en las mismas, lo cual es físicamente imposible.
La energía absorbida por la bobina es almacenada en el campo magnético.
Siendo Li = NΦ obtenemos:
Al igual que en el condensador, la energía absorbida por la bobina ideal puede ser, más tarde, cedida.
Bobinas en Acoplamiento Magnético
Un par de bobinas acopladas es un ejemplo de elemento con cuatro terminales (cuadripolo), de los vistos con anterioridad (Fig. 2), con su correspondiente definición de potencia (ecuaciones 4 y 5).
A partir de su ecuación de definición (Fig. 6a):
Para las referencias de las dos bobinas acopladas de la Fig. 6a y de la expresión de la potencia total entrante, tenemos:
expresión que se puede poner de la forma:
Integrando y suponiendo que i1(-∞) = i2(-∞) = 0 se obtiene:
La energía absorbida es almacenada en el campo magnético, como en el caso de una bobina, pudiendo ser cedida más tarde.
Si para todo valor de t es i2(t) = 0, se obtiene:
es decir, el sistema se comporta en este caso como una sola bobina, lo que era de esperar, puesto que en una de ellas no hay corriente, no produciendo flujo la misma. Si las referencias de polaridad son las de la Fig. 6b, se puede obtener que, en este caso:
(puede probarse que en cualquier caso, siempre se tiene que w(t)≥0.
Transformador Ideal
Para las referencias de la Fig. 7 tenemos:
Ecuación de definición:
Potencia total entrante:
Sustituyendo (26) en (27) se obtiene:
y, por tanto,
es decir, en todo instante, la potencia entrante por el primario es igual a la potencia saliente por el secundario.
Por otro lado,
En consecuencia, el transformador ideal no absorbe ni cede energía, es decir, la transferencia de potencia de un devanado a otro es total.
Fuente de Tensión Ideal
Sea (Fig. 8) una fuente de tensión ideal que se carga con una resistencia R.
Siendo:
y la potencia suministrada por la fuente:
Para e = cte., la gráfica representativa de la dependencia de p respecto de R es (Fig. 9) una hipérbola equilátera, referida a sus asíntotas.
Para R→0 , p→∞. Vemos pues, que una fuente de tensión ideal no tiene limitación en cuanto a la potencia que puede suministrar.
Fuente de Intensidad Ideal
Para una fuente de intensidad ideal con carga resistiva (Fig. 10) se verifica:
Se observa que p→∞ cuando G→0 (circuito abierto).
Fuente de Tensión Real
En el caso de que la fuente fuese real (Fig. 11), se tendría, al conectar una carga resistiva R:
La potencia suministrada a R es:
Para R = 0 (cortocircuito) y para R = ∞ (circuito abierto) p = 0, es decir, la fuente no suministra potencia a la carga. Entre esos límites, la potencia suministrada es siempre finita y positiva. Para eg = cte., p alcanza un máximo R = Rg (posteriormente se verá esto como el teorema de máxima transferencia de potencia a la carga). El rendimiento η es la relación entre la potencia recibida por la carga R y la suministrada por eg, parte de la cual se pierde en Rg.
Se tiene, pues:
Para R = Rg se tiene η = 0.5, es decir, cuando se transfiere la máxima potencia, el rendimiento es de 0.5.
En la Fig. 12 se representan p y η como funciones de R.
Fuente de Intensidad Real
Para una fuente real resistiva, con carga del mismo carácter (Fig. 13), se tiene:
Luego, la potencia entregada a G será:
Cuando G = 0 (circuito abierto) y cuando G = ∞ (cortocircuito) P = 0. Para cualquier otro valor de G, la potencia recibida por la carga es siempre finita y alcanza un valor máximo
para G = Gg.
La expresión del rendimiento es:
que se hace igual a 0.5 cuando G = Gg, es decir, cuando se transmite la máxima potencia a la carga.
Las gráficas de las ecuaciones (37), (38) y (40) son las mismas que las de las figuras 9 y 12, sin más que sustituir R por G y eg por ig.
Resistencia
Para las referencias tomadas en la Fig. 3 tenemos:
Ecuación de definición:
Potencia entrante:
Sustituyendo (6) en (7) se llega a:
y, por tanto:
La energía absorbida por una resistencia es siempre positiva y es disipada en forma de calor (Ley de Joule).
Condensador
A partir de su ecuación de definición:
para las referencias de la Fig. 4 y de la expresión de potencia entrante, obtenemos:
luego:
En todo condensador físico u(-∞) = 0, luego:
Como se observa, el valor de la energía del condensador en uun instante determinado solo depende del valor de la tensión en dicho instante, pero no de la forma como varía ésta. Igualmente, podemos comprobar que la tensión del condensador no puede variar bruscamente, ya que, si así fuera, también lo haría la energía, lo cual implicaría una potencia infinita en el punto de discontinuidad, cosa físicamente imposible.
Toda energía absorbida por el condensador es almacenada en el campo eléctrico existente entre sus armaduras. Siendo q = C·u, podemos obtener otras expresiones:
Por otro lado, todo condensador es capaz de ceder energía a costa de la que ya había absorbido previamente. Ello ocurre, por ejemplo, en la descarga de un condensador a través de una resistencia.
Bobina Ideal
Para las referencias de la Fig. 5 tenemos:
Ecuación de definición:
Potencia entrante:
por tanto:
En toda bobina física i(-∞) = 0, luego:
La ecuacion 18 nos muestra que el valor de la energía absorbida por la bobina en un instante dado sólo depende del valor de la intensidad en dicho instante y no de la forma como varía ésta. Por otro lado, comprobamos que la intensidad de la bobina no puede presentar discontinuidades, ya que si fuera así, también las presentaría la energía, con el consiguiente valor infinito de la potencia en las mismas, lo cual es físicamente imposible.
La energía absorbida por la bobina es almacenada en el campo magnético.
Siendo Li = NΦ obtenemos:
Al igual que en el condensador, la energía absorbida por la bobina ideal puede ser, más tarde, cedida.
Bobinas en Acoplamiento Magnético
Un par de bobinas acopladas es un ejemplo de elemento con cuatro terminales (cuadripolo), de los vistos con anterioridad (Fig. 2), con su correspondiente definición de potencia (ecuaciones 4 y 5).
A partir de su ecuación de definición (Fig. 6a):
Para las referencias de las dos bobinas acopladas de la Fig. 6a y de la expresión de la potencia total entrante, tenemos:
expresión que se puede poner de la forma:
Integrando y suponiendo que i1(-∞) = i2(-∞) = 0 se obtiene:
La energía absorbida es almacenada en el campo magnético, como en el caso de una bobina, pudiendo ser cedida más tarde.
Si para todo valor de t es i2(t) = 0, se obtiene:
es decir, el sistema se comporta en este caso como una sola bobina, lo que era de esperar, puesto que en una de ellas no hay corriente, no produciendo flujo la misma. Si las referencias de polaridad son las de la Fig. 6b, se puede obtener que, en este caso:
(puede probarse que en cualquier caso, siempre se tiene que w(t)≥0.
Transformador Ideal
Para las referencias de la Fig. 7 tenemos:
Ecuación de definición:
Potencia total entrante:
Sustituyendo (26) en (27) se obtiene:
y, por tanto,
es decir, en todo instante, la potencia entrante por el primario es igual a la potencia saliente por el secundario.
Por otro lado,
En consecuencia, el transformador ideal no absorbe ni cede energía, es decir, la transferencia de potencia de un devanado a otro es total.
Fuente de Tensión Ideal
Sea (Fig. 8) una fuente de tensión ideal que se carga con una resistencia R.
Siendo:
y la potencia suministrada por la fuente:
Para e = cte., la gráfica representativa de la dependencia de p respecto de R es (Fig. 9) una hipérbola equilátera, referida a sus asíntotas.
Para R→0 , p→∞. Vemos pues, que una fuente de tensión ideal no tiene limitación en cuanto a la potencia que puede suministrar.
Fuente de Intensidad Ideal
Para una fuente de intensidad ideal con carga resistiva (Fig. 10) se verifica:
Se observa que p→∞ cuando G→0 (circuito abierto).
Fuente de Tensión Real
En el caso de que la fuente fuese real (Fig. 11), se tendría, al conectar una carga resistiva R:
La potencia suministrada a R es:
Para R = 0 (cortocircuito) y para R = ∞ (circuito abierto) p = 0, es decir, la fuente no suministra potencia a la carga. Entre esos límites, la potencia suministrada es siempre finita y positiva. Para eg = cte., p alcanza un máximo R = Rg (posteriormente se verá esto como el teorema de máxima transferencia de potencia a la carga). El rendimiento η es la relación entre la potencia recibida por la carga R y la suministrada por eg, parte de la cual se pierde en Rg.
Se tiene, pues:
Para R = Rg se tiene η = 0.5, es decir, cuando se transfiere la máxima potencia, el rendimiento es de 0.5.
En la Fig. 12 se representan p y η como funciones de R.
Fuente de Intensidad Real
Para una fuente real resistiva, con carga del mismo carácter (Fig. 13), se tiene:
Luego, la potencia entregada a G será:
Cuando G = 0 (circuito abierto) y cuando G = ∞ (cortocircuito) P = 0. Para cualquier otro valor de G, la potencia recibida por la carga es siempre finita y alcanza un valor máximo
para G = Gg.
La expresión del rendimiento es:
que se hace igual a 0.5 cuando G = Gg, es decir, cuando se transmite la máxima potencia a la carga.
Las gráficas de las ecuaciones (37), (38) y (40) son las mismas que las de las figuras 9 y 12, sin más que sustituir R por G y eg por ig.


















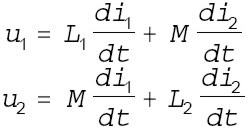











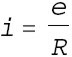

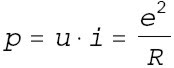























0 comments:
Publicar un comentario